import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
da = pd.read_csv("https://raw.githubusercontent.com/joanby/estadistica-inferencial/master/datasets/nhanes_2015_2016.csv")
print (f"median : {np.nanmedian(da.BPXSY2)}")
print (f"mean : {np.nanmean(da.BPXSY2)}")
print (f"Standard-Deviation : {np.std(da.BPXSY2,ddof=1)}")
print (f"max : {np.max(da.BPXSY2)}")
print (f"IQR : {np.subtract(*np.nanpercentile(da.BPXSY2, [75, 25]))}")

median : 122.0
mean : 124.78301716350497
Standard-Deviation : 18.527011720294997
max : 238.0
IQR : 22.0

Standard Deviation = 根號(均差的平方和的平均) = 根號(平方和的平均 - 平均的平方)

均差 : (1-4),(3-4),(4-4),(4-4),(3-4),(9-4)
均差的平方和 = ((1-4)^2+(3-4)^2+(4-4)^2+(4-4)^2+(3-4)^2+(9-4)^2)
均差的平方和的平均  = ((1-4)^2+(3-4)^2+(4-4)^2+(4-4)^2+(3-4)^2+(9-4)^2)/6
根號(均差的平方和的平均) = (((1-4)^2+(3-4)^2+(4-4)^2+(4-4)^2+(3-4)^2+(9-4)^2)/6)^0.5

平方和的平均 = (1^2+3^2+4^2+4^2+3^2+9^2)/6
根號(平方和的平均 - 平均的平方) = ((1^2+3^2+4^2+4^2+3^2+9^2)/6 - 4^2)^0.5

1,3,3,4,4,9 
min = 1
max = 9
Mean(平均數) = (1+3+3+4+4+9)/6 = 4
Q1(25%) = 3
median(50%) = (3+4)/2 = 3.5
Q3(75%) = 4
IQR = Q1-Q4 = 1
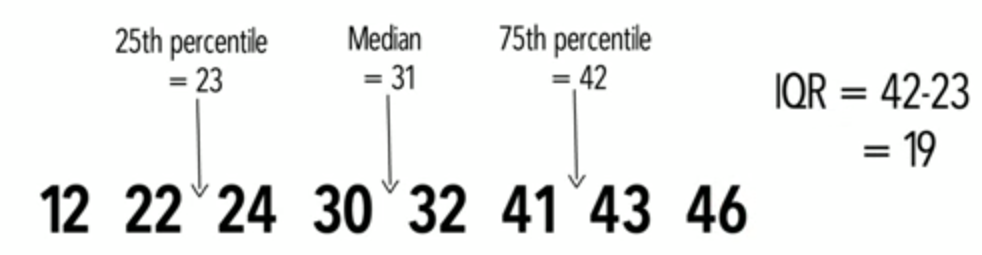
IQR(interquartile range)

             median
    min    Q1   Q3                 max
            +-|-+
    |-------| | |-------------------|
            +-|-+
			
+---+---+---+---+---+---+---+---+---+---+
0   1   2   3   4   5   6   7   8   9  10

standard score is: (Observation - Mean) / Standard Deviation

μ︰population mean

x̅︰sample mean / estimate of population mean

σ︰population standard deviation（或簡稱為population sd）

s︰sample standard deviation / estimate of population standard deviation